Ant Colony Optimization to solve Travelling Salesman Problem in Java
Travelling Salesman Problem (TSP)
The travelling salesman problem (TSP) try the solve the following problem: “For a given list of cities (vertices) and the distances beteween each pair of cities (edges), what is the shortest route that visits each city only one time and return to the origin city?”. It is an NP-hard problem in combinatorial optimization, important in operations reasearch and theorical computer science.
In the theory of computational complexity the deterministic algorithms that execute all posibilities to try to find the best route needs a long (very long) time to find the solution. The main point is that, the complexity of the problem increase exponentially with the number of cities, so a metaheuristic that do not guarantee the best solution but can found an suboptimal solution is a good alternative to solve the TSP in a acceptable time.
The following image is an example of the TSP problem resolved:

Ant Colony Optimization (ACO)
Ant colony optimization is a meta-heuristic used to solve complex discret problems, normally used to search good solutions in graph systems. The principles of ACO are based on the natural behavior of ants, that in their daily life, one of the tasks that ants have to perform is search for food, in the region near of their nest. While ants are searching for food, their deposit on the ground a chemical substance called pheromone used to two main objectives: 1) a way to memorize how to back to the nest and 2) and lets a trail for that the other ants can calculate the next step decisions. The second objective is the most important part to the ants find good optmized path between the nest and the food source. The pheromone laid in the ground by the ants create a specie of network where de edges quality is relative to the amount of the pheromone deposited, this system is used probabilistically to ants takes decisions in the environment.
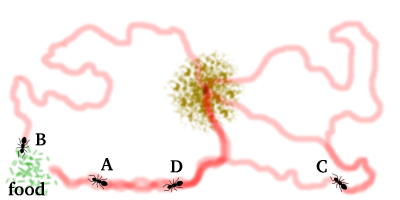
The communication between ants is made indirect by stigmergy with the environment, if the path has large concentration of pheromone, this is probably due to its shorter length that allowed ants to travel faster, resulting in a large number of travels through the path therefore with much more ants depositing pheromone on it. Furthermore, over time the evaporation on the ground reduce the intensity of path pheromone, the evaporation make ants forgot path with low quality and increase the capacity of the ants to explore new paths. The image below gives an example of the ant system:
Canonical Ant Colony Optimization (ACO) algorithm
Meanwhile, a good number of improvements were inserted in the ants system (AS) with extensions as elitism, ranking, bounding, etc. Nevertheless, the most important development is the description of the Ant Colony Optimization Metaheuristic by Dorigo and Di Caro. The canonical main part of the algorithm is given below:
Algorithm 1 - Pseudo-code for Ant Colony Optimization
Initialize parameters
Initialize pheromone trails
Create ants
while Stopping criteria is not reached do
Let all ants construct their solution
Update pheromone trails
Allow Daemon Actions
end while
The detail of the ACO is the Daemon Actions that can perform problem specific operations or centralized operations, which use global knowledge of the solutions. Examples of operations that can be executed in Daemon Actions are: control the feasibility of each solution, give extra pheromone quantity to the best solutions, use some local search routine to improve the solutions, etc.
ACO algorithm have some building blocks that need to be understanded, and in some cases modeled to specific problems to obtain best results. The following building blocks determine the success of the algorithm:
- Method chosen to construct the solutions
- Heuristic information
- Pheromone updating rule
- Transition rule and probability function
- Parameters values
- Termination condition
How to use
The project was constructed with maven, so to see the code working just open the project in your favorite Java IDE and run the main class (Program.java). Note that the main classe is pointing to the path of the tsp folder inside the repository, so take care for that the path is configured correctly.
A little description of the classes of the algorithm are given below:
- Ant: Model an ant, has the current state of the ants (tour information) and has the logic to process the state transition.
- Environment: Model the environment, contains the information about the graph and the pheromone deposited by the ants.
- Parameters: Contains the global parameters used by the ACO
- Program: call the main building blocks of the ACO (Algorithm 1).
- Statistics: calculate the algorithm evolution statistics, ex: best tour found.
- TspReader: create a instance of the TSP problem.
- Visualizer: plot a graph with the vertices and edges showing the best tour found.
Conclusions
We can conclude that the meta-heuristics are very useful to solve very complex problems with a low cost and time consumption. And even using a very simple implementation of the ACO without any extension cited above, the results were very significant showing a good aproximation of the best solution cost cited in the TSP site.
More details about the project can be found here.
